Kaufman’s adaptive moving average
This lesson will cover the following
- Definition
- Calculation
- Interpretation
Developed by Perry Kaufman, Kaufman’s Adaptive Moving Average is designed not only to function as a moving average but also to track the level of noise in the trend and adjust accordingly. It automatically changes its speed according to market volatility.
The AMA is used as a replacement for ordinary moving averages and, when it was introduced in 1995, it proved superior to previous attempts to create an intelligent moving average because it offered greater user control.
Basically, when the market is trending strongly and there are only minor counter-trend moves (pullbacks), there is very little noise. In such cases you would prefer the MA to closely follow the price action, so you would want it to have a shorter look-back span.
On the other hand, if the market is range-bound and dominated by bars that offset each other, you need a moving average with a longer look-back period to smooth out the action and thus avoid false signals.
- Trade Forex
- Trade Crypto
- Trade Stocks
- Regulation: NFA
- Leverage: Day Margin
- Min Deposit: $100
Upgrade
Kaufman tweaked the Exponential Moving Average with an algorithm that adjusts the EMA’s smoothing constant in relation to the ratio of market direction to volatility, making it responsive to both trend and volatility. Here is the formula from which the AMA is derived:
AMA = C * [close(t) – AMA(t-1)] + AMA(t-1), where C represents the adaptive component of the smoothing constant. There are several calculations required to determine C, but we will not list them here to keep things simple.
It is more important to realise that Kaufman’s Adaptive Moving Average excels because it can respond to dynamic shifts in market conditions, which is a major advantage compared with trading strategies based on moving averages with fixed look-back periods. Moreover, apart from using the KAMA as a stand-alone indicator, it can also be used to smooth other indicators.
Like other members of the moving-average family, Kaufman’s AMA acts as a strong support/resistance level that generates with-trend entry signals upon contact, as well as exit signals when a trend reversal is evident. The screenshot below shows the difference between a Simple Moving Average, an Exponential Moving Average and Kaufman’s Adaptive Moving Average.
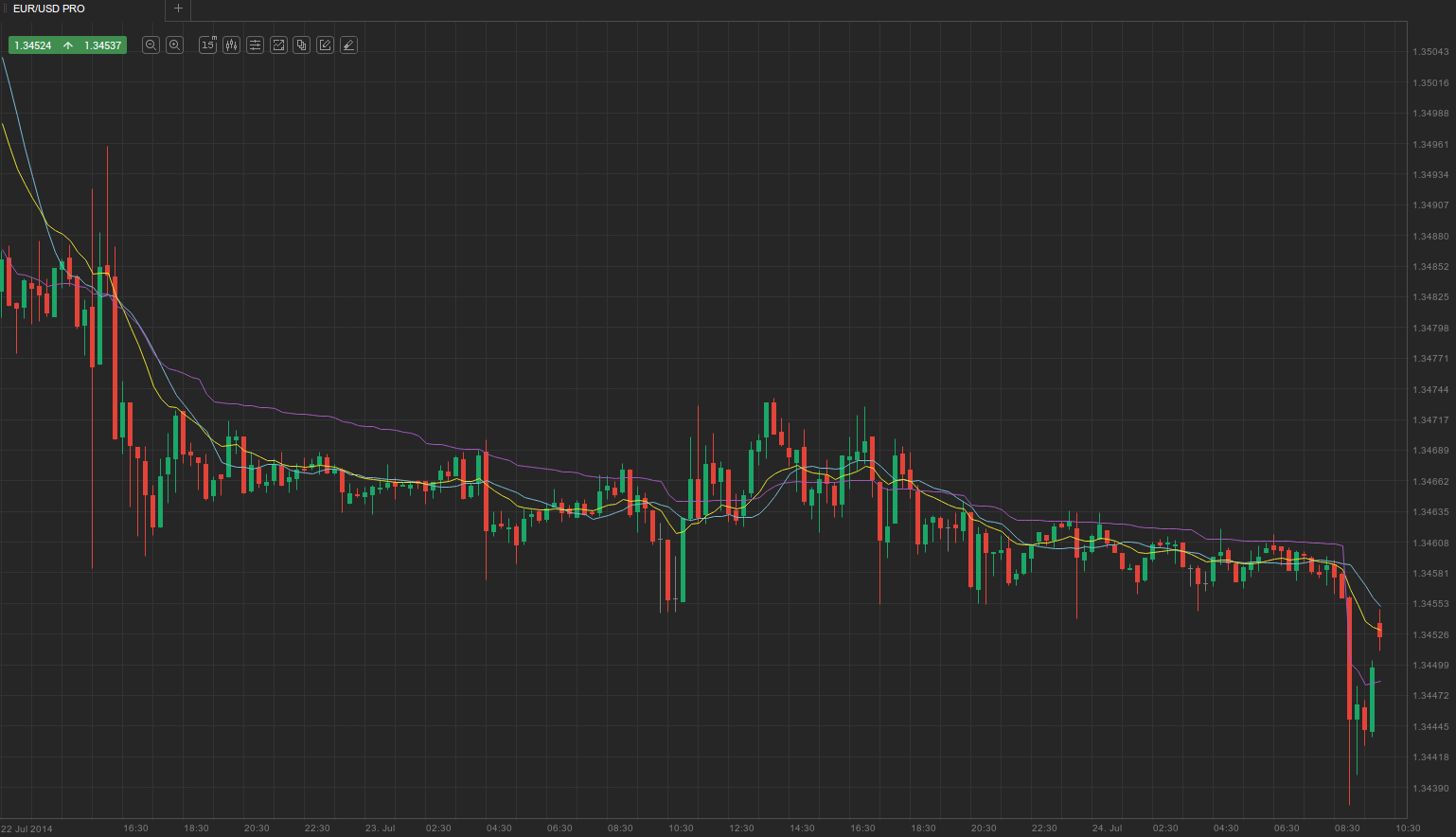
Plotted in light blue is a 14-period Simple Moving Average, while the 14-period EMA is coloured yellow. As you can see, Kaufman’s Adaptive Moving Average (purple line) is relatively flat for most of the time because the market remains in a tight trading range within the larger time frame’s bearish trend. Consequently, it produces fewer false entry signals within the consolidation area.
